This is the first post in a series of engineering topics for non-engineers that I plan to write. This topic is Kinetic Energy, and is likely the most relevant to things we all do, are involved in, or are subject to.
There’s two types of energy, potential and kinetic. Potential energy can be a compressed spring, a weight up on a shelf, a charged capacitor, a magnetic field, or the unburned powder in a .45 ACP cartridge. Potential energy just sits there, till it goes off and zings something. Kinetic energy you can see coming, it’s in anything that’s moving. Kinetic energy is fun and exciting.
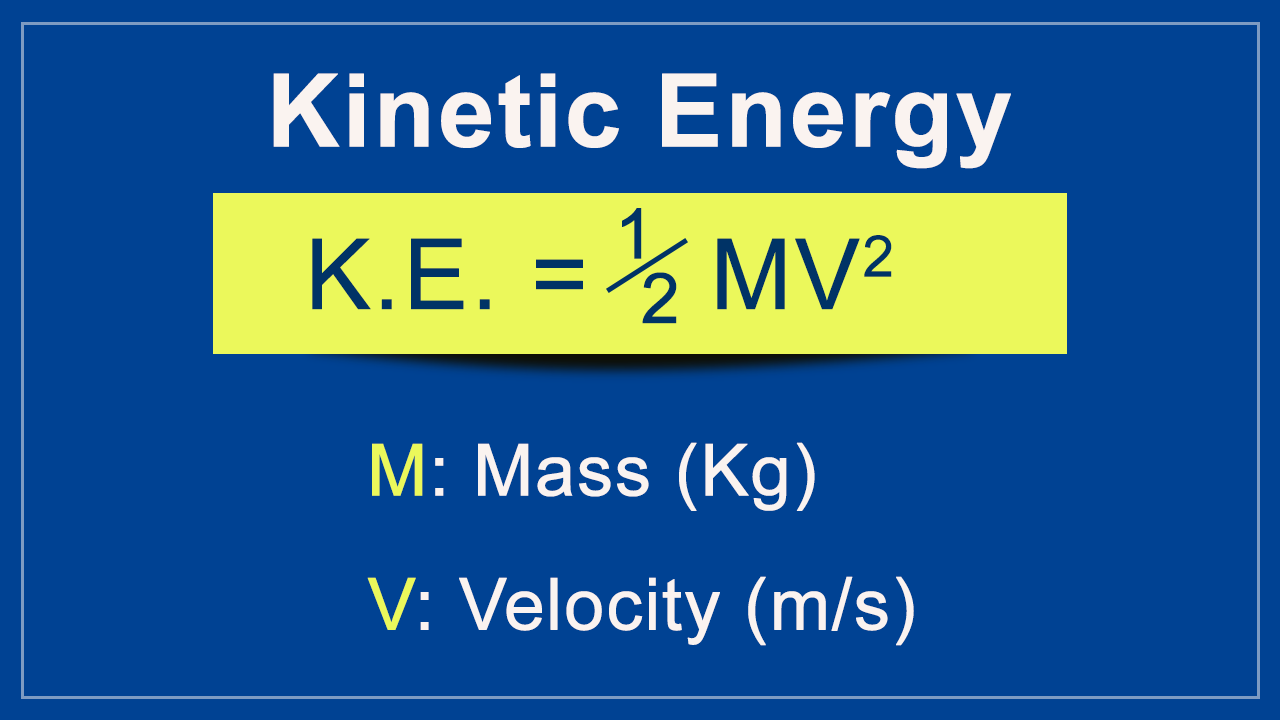
The formula for Kinetic Energy (KE) is one half Mass times velocity squared, 0.5*M*V^2. There will not be a test, but note the value is proportional to the velocity squared. You add 10% to the speed and the KE goes up 21% (1.1*1.1=1.21), a 41% increase in speed doubles your KE, doubling your speed quadruples your KE, etc. You get a lot of bang for your buck.
Say you want to knock something down, downrange. KE is your friend, adding velocity to the bullet adds a lot more KE that’ll be delivered to the target. If you’re driving, it’ll work against, you. At higher velocities, you have disproportionately more KE to get rid of to come to a stop, not to mention less time to do it and your car/truck’s braking ability doesn’t increase. 10% more speed, you need to brake 21% more, etc.
Wind speed and hurricanes, it’s the same. Small increase in wind speed, bigger increase in KE in anything wind borne.
Punches deliver KE to a target. These really benefit from an increase in speed for a multitude of reasons. First, for the reasons stated above, an increase in speed delivers a bigger increase in KE, secondly, a faster punch is harder to block or avoid and a punch that connects is much more useful than a punch that doesn’t (unless that punch is setting the target up for a followup punch).
Rotating masses have KE too, same relationship to angular velocity, just much less likely to be encountered daily.
If you have any questions, ask them in the comments, I’ll (try) to answer them.
Kinetic Energy for Non-Engineers
10 Comments
Leave a Reply
Support Men Of The West
Latest from Culture
Livy, A Narrator of History
"Even in his own time he was known as the greatest of Roman historians."
“The Castle of Time” by Lord Dunsany
Presently there was a stir in one of the houses, and a bat flew out of the door into the daylight, and three mice came running out of the doorway down the
A Compact Renewed
It was the fourth of July, 1809, and thunderous, close evening. In Lobau, the largest of the five islands on the Danube, where were the imperial headquarters, the huge machinery of war,
A Memory of Robert E. Lee
"Everyone obeyed him, not because they feared but because they loved him."
The Venerable Bede
"Arising from the gloom of a dark age, he is still considered one of the most illustrious of the learned men of England."
Is a spinning flywheel potential or kinetic?
A spinning flywheel contains kinetic energy. The physics are the same, so you’ll recognize the similarity in the formula to calculate it, but ton account for the increasing velocities, the furthers away from the axis of rotation the variables are different, similar, but different.
To calculate kinetic energy of a flywheel (or any rotating mass) the formula is KE=1/2 I w^2, which follows the same format as KE for linear motion.
I being the Moment of Inertia, and
W being the angular velocity in radians per second.
How is the amount of kinetic energy expressed? Say I’ve got 16 ounces of mass at a velocity of 10 miles per hour, then per the formula .5*16*10squared = .5*16*100 = 800. 800 what?
0.5 (unitless) * 16 ounces * 10 miles/hour * 10 miles/hour = 800 ounce miles squared per second squared. I don’t think this unit has a formal name. Munging into the metric system (and assuming ounces (a unit of force) corresponds to mass)…
0.5 (unitless) * 0.454 kg * 4.47 m/s * 4.47 m/s ~= 4.532 kg*m^2/s^2. This measures energy. And that unit is called a Joule. One Joule is enough energy to accelerate 1 kg of mass to a speed of one meter per second, accelerating over a distance of one meter in the time of one second.
Don’t give in to these Metric system globalists trying to make us give up our Imperial units, Ethan.
Mr. Heron’s math is right on the mark though. 16 ounces mass = 1 pound mass. One mile is equal to 5280 feet. One hour is equal to 3600 seconds. It is easier to do your converting right now, rather than deal with it later.
So 0.5*1 pound mass*(14.6 ft/sec)^2 is equal to (107 pounds mass * ft^2) / (sec^2). Now, the goofy part about us using “pound” for both mass and force catches up to us. One pound force is equal to 32.174 (pound mass * foot) / (sec^2). Divide our 107 number by 32.174, and kill the units that cancel one another.
This leaves us with the much more ballistically recognizable: 3.34 foot pounds force. Which is equal to Mr. Heron’s 4.532 Joules.
And then we use slang again and just say: 3.34 foot pounds.
We expect the Imperial unit users to be more intelligent than those grubby metric folk, and able to figure out what we are saying.
Agreed. We do not support commie measurements in these parts.
What if I told you that US customary units are based on the metric system…
And have been since 1893?
The U.S. was Great Britain before we figured out something better too. An affectionate pat on the head for the cute system that went before us. Thanks metric!
Subterfuge to keep the commies happy